Best of Seven Jul 2022

Evenly Matched Teams

If the two teams are evenly matched, then we say the probability that Team A wins each game is 0.50. The probability that Team B wins each game is also 0.50, and the sum of these two probabilities is 1.0 as expected.

The question here is, what is the likelihood of each possible playoff outcome:

• 4-0 Team A wins
• 4-1 Team A wins
• 4-2 Team A wins
• 4-3 Team A wins and

• 4-0 Team B wins
• 4-1 Team B wins
• 4-2 Team B wins
• 4-3 Team B wins

Team A is Stronger

If the two teams are not evenly matched, then let’s say the probability that Team A wins each game is P. The probability that Team B wins each game is now therefore Q = 1 – P, and the sum of the probabilities P + Q = 1.0 as expected.

For example, if the probability that Team A wins each game is P = 0.81, then the probability that Team B wins each game is Q = 1 – P = 0.19.

Again, the question is, what is the likelihood of each possible playoff outcome:

• 4-0 Team A wins,
• 4-1 Team A wins,
• 4-2 Team A wins,
• 4-3 Team A wins, and

• 4-0 Team B wins,
• 4-1 Team B wins,
• 4-2 Team B wins,
• 4-3 Team B wins?

Discussion

This answer to this problem is relatively easy to discuss yet somewhat complex to calculate, Fortunately, it can be broken down into several similar parts.

Series Goes 4-0 or 0-4

An easy start: if Team A wins in 4 straight, then the probability is simply $$ {P^4} = 0.81^4 = 0.430 $$

And similarly: if Team B wins in 4 straight, then the probability is simply $$ {Q^4} = 0.19^4 = 0.001 $$ in this example very unlikely.

Series Goes 4-1 or 1-4

Now, if Team A is to win the series 4-1, then after 4 games, they must be up 3-1 just before the 5th game in the series. That means there is one loss in the 4 games played and there are only 4 ways that can happen.

Therefore the probability is $$\left[{P^4}\cdot{Q}\right]\cdot\left[{_4}{{C}_1}}\right] = ({0.81^4}\cdot {0.19})\cdot {4} = 0.327$$

Explanation:

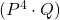• $ ({P^4}\cdot{Q}) $ is the one-time probability of Team A winning 4 games and Team B winning one game.
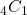• $ {_4{{C}_1}} $ is the number of combinations in which one team wins 3 games and the other wins only one game.
  Click for explanation of combinations

Similarly, if Team B is to win the series 4-1, then after 4 games, they must be up 3-1 just before the 5th game in the series. Therefore the probability is $$\left[{Q^4}\cdot{P}\right]\cdot\left[{_4}{{C}_1}}\right] = ({0.19^4}\cdot {0.81})\cdot {4} = 0.004$$

Series Goes 4-2 or 2-4

If Team A is to win the series 4-2, then after 5 games, they must be up 3-2 just before the 6th game in the series. That means there are 2 losses in the 5 games played and there are only 10 ways that can happen.

So we have established the pattern, if Team A is to win the series $4-\mathbf{X}$, the probability is $$\left[{P^4}\cdot{Q^\mathbf{X}}\right]\cdot\left[{_{(\mathbf{X}+3)}{{C}_\mathbf{X}}}\right]$$

Likewise, if Team B is to win the series $\mathbf{X}-4$, the probability is $$\left[{Q^4}\cdot{P^\mathbf{X}}\right]\cdot\left[{_{(\mathbf{X}+3)}{{C}_\mathbf{X}}}\right]$$

$$ _{(\mathbf{0}+3)}{{C}_\mathbf{0} = \prescript{_3}{{C}_{0}} = \frac {3!}{{3!}\cdot{0!}} = 1 $$
$$ _{(\mathbf{1}+3)}{{C}_\mathbf{1} = \prescript{_4}{{C}_{1}} = \frac {4!}{{3!}\cdot{1!}} = 4 $$
$$ _{(\mathbf{2}+3)}{{C}_\mathbf{2} = \prescript{_5}{{C}_{2}} = \frac {5!}{{3!}\cdot{2!}} = 10 $$
$$ _{(\mathbf{3}+3)}{{C}_\mathbf{3} = \prescript{_6}{{C}_{3}} = \frac {6!}{{3!}\cdot{3!}} = 20 $$

Observation

Notice that compared to a single game, a seven game series increases the probability that the strong team wins the series. For example, with P = 0.81, as shown above, the probability that Team A wins the series is calculated at 0.972. Note further that the probability that Team B wins the series decreases from 0.19 to only 0.028.

Using Odds:

The single game had odds of 81:19 or about 4:1 whereas the series has odds of 972:28 or about 35:1.

Plots

See the plots of all possible outcomes for all probabilities:

$$ P \mid 0 < P < 1 $$ Example probabilities are given for the specific case where $ P = 0.81 $. Live Plot

Click for Best of Seven Live Chart

Using PLOTLY live plots

Each chart series can be toggled off and on

by clicking its legend entry.

On a desktop device, reset the chart to full scale

by reloading the web page.

On a mobile device, reset the chart to full scale

by double tapping.

Static Plots

Reference

Best of Seven Outcome Probability Dec 2020

Bonus Calculations (added June 2024)

---

One game played

What if one game has already been played and Team A won that game; now what is the probability of each series arrangement?

If Team A is to win the series $4-\mathbf{X}$, the probability is $$\left[{P^3}\cdot{Q^\mathbf{X}}\right]\cdot\left[{\prescript{_{(\mathbf{X}+2)}}{{C}_\mathbf{X}}}\right]$$

Two games played (imagine the 2024 Celtics in such a situation)

What if two games have already been played and Team A won both games; now what is the probability of each series arrangement?

If Team A is to win the series $4-\mathbf{X}$, the probability is $$\left[{P^2}\cdot{Q^\mathbf{X}}\right]\cdot\left[{\prescript{_{(\mathbf{X}+1)}}{{C}_\mathbf{X}}}\right]$$

Closed form solution for 7-games series

Let’s add another variable.

   Let’s say $\mathbf{Y}$ games have been played and that Team A won those games.

Now what is the probability of each series arrangement?

If Team A is to win the series $4-\mathbf{X}$, the probability is $$\left[{P^{(4-\mathbf{Y})}\cdot{Q^\mathbf{X}}\right]\cdot\left[{_{(\mathbf{X}+3-\mathbf{Y})}{{C}_\mathbf{X}}}\right]$$

If Team B is to win the series $\mathbf{X}-4$, the probability is $$\left[{P^{(\mathbf{X}-\mathbf{Y})}\cdot{Q^4}\right]\cdot\left[{_{(\mathbf{X}+3-\mathbf{Y})}{{C}_{(\mathbf{X}-\mathbf{Y})}}}\right]$$

Closed form for N-game series solution

And finally, what is the probability of each series arrangement, where

   $\mathbf{N} = \text{number of games in the series}$

   Again, $\mathbf{Y}$ games have been played and Team A has won those games.

Two more new variables:

   Let $\mathbf{L} = \lfloor N/2 \rfloor$, floor function
   Let $\mathbf{M} = \lceil N/2 \rceil$, ceiling function

If Team A is to win the series $\mathbf{M}\text{ games to }\mathbf{X}$, the probability is $$\left[{P^{(\mathbf{M}-\mathbf{Y})}\cdot{Q^\mathbf{X}}\right]\cdot\left[{_{(\mathbf{X}+\mathbf{L}-\mathbf{Y})}{{C}_\mathbf{X}}}\right]$$

If Team B is to win the series $\mathbf{X}\text{ games to }\mathbf{M}$, the probability is $$\left[{P^{(\mathbf{X}-\mathbf{Y})}\cdot{Q^\mathbf{M}}\right]\cdot\left[{_{(\mathbf{X}+\mathbf{L}-\mathbf{Y})}{{C}_{(\mathbf{X}-\mathbf{Y})}}}\right]$$