Something about calculus and Sympy is lovable
I find it effective to use closed form solutions and to be able to develop/verify special cases using well-known (and well worn) formulas.
I built a Jupyter notebook. Here is my summary of the contents.
- Given a beam with fixed ends and a single concentrated load
:
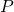(a) Write the equation for the reactions,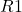
, 
, 
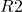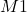, and 
,
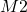(b) Plot the reaction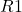 for all possible locations of ,
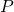(c) Build a function, using indefinite integration to determine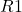 and 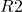for a partial uniform moment, 
,
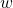(d) Build a function, using definite integration to determine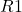 and 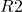for a partial uniform moment, ,
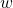(e) Consider the point load,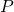, located at a distance, 
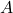, from the left support. What location 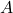would result in the maximum moment at the left support?,
(f) Consider a partial uniform load, applied to the beam only over a distance L/2, what location of the uniform load would result in the maximum moment at the left support?,
(g) Determine the solution of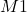 for any arbitrary partial uniform loading, ,
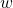(h) Determine the solution of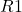 for any arbitrary partial uniform loading, ,
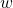(Bonus 1) Determine the solution of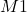 for various ‘checkered’ uniform loadings, ,
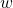(Bonus 2) Determine the solution of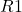 for various ‘checkered’ uniform loadings, .
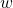My Jupyter Notebook
Live Charts
