Homepage
>
Mathematics
>
The Analog Clock Jul 2022

The Analog Clock Jul 2022

25 or 6 to 4
– Robert Lamm, Chicago

Haven’t we all looked at the clock face and wondered about the magical times where the hands cross?

The mathematically curious probably even considered calculating the crossing times.

I know of two ways to calculate the crossing times and both are easy.

(1) Arithmetic (with insight)
(2) Algebra

Here are two bonus questions:

At what times are the two hands perpendicular to each other?
At what times are the two hands opposite each other?

Arithmetic

Observe the clock hand movements for a while and notice that after 12:00, the minute and hour hands cross 11 times in 12 hours.

Therefore, the crossings divide the 12 hours into 11 equal parts or intervals of time. Remember that each hand moves at a constant angular rate (steady circular movement).

Therefore, each interval must be $\frac{12}{11}$ hours.

$1.0909$ hours at the 1st crossing

$2.1818$ hours at the 2nd crossing

And so forth.

https://www.roomrecess.com/Tools/InteractiveClock/play.html

Algebra

Let’s define terms.

$2\pi$ : angle measure of a full circle; measured from straight-up 12:00

$H$ , $H-1$ , $H-2$ , etc: number of hours

$N$ : crossing count

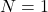$N=1$ for the crossing after 1:00
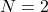$N=2$ for the crossing after 2:00
And so forth

The hour hand completes a circle in 12 hours, therefore:

the angular rate of the hour hand is $\frac {2\pi}{12}$
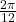
the angular location of the hour hand is $\theta = \frac {2\pi}{12} \cdot (H)$

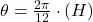
The minute hand completes a circle in 1 hour, therefore:

the angular rate of the minute hand is therefore $2\pi$
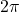
the angular location of the minute hand is $\theta = 2 \pi \cdot (H-N)$ ;
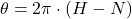the expression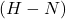 $(H-N)$ provides an angular position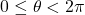 $0 \leq \theta < 2\pi$

Setting the two locations equal after one hour, the equation is:

$\frac{2\pi}{12} (H) = 2 \pi \cdot (H-1)$

$H = 12 \cdot (H-1)$

$H = 12H-12$

$12 = 11H$

$H = 12/11\textrm{ hours}$

$\therefore 1.0909\textrm{ for just past 1:00}$

Setting the two locations equal after two hours, the equation is:

$\frac{2\pi}{12} (H) = 2 \pi \cdot (H-2)$

$H = 12 \cdot (H-2)$

$H = 12H-24$

$24 = 11H$

$H = 24/11\textrm{ hours}$

$\therefore 2.1818\textrm{ for just past 2:00}$

Therefore, the general solution after $N$ hours is:

$\frac{2\pi}{12} (H) = 2 \pi \cdot (H-N)$

$H = 12 \cdot (H-N)$

$H = 12H-12N$

$12N = 11H$

$H = \frac {12N}{11}\textrm{ hours}$

$\therefore 1.0909N \textrm{ for just past N o'clock}$

Leave a Reply Cancel reply