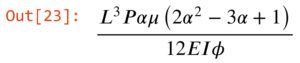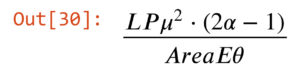Asymmetric Frame Loading Jul 2022

In remembrance of Dr. Terry Kohutek, Texas A & M, Professor of Civil Engineering

Well-respected teacher

https://www.dignitymemorial.com/obituaries/college-station-tx/terry-kohutek-5194499

Many years ago (1989, a third of a century ago), I was in an oral exam at TAMU; several civil engineering faculty were in the exam room.

Dr. Kohutek asked about a pin-supported frame subjected to a single concentrated vertical load:

The frame itself is symmetric.
Consider, he said, the load to be over the center of the beam; no sidesway deflection is expected — symmetry.
Next he said, consider the load to be over the left column; no sidesway deflection is expected (due to flexural deformation).
Next he said, consider the load to be over the right column; again no sidesway deflection is expected (again, due to flexure deformation).
Now, place the load just to the right of the left column.

What is the expected horizontal displacement for this loading?

Which direction is the horizontal deflection?

I answered — incorrectly — that the deflection would be toward the left. Dr. Kohutek said the deflection would be toward the right. There was a vigorous discussion with more faculty saying left than right.

After the exam, Kohutek checked the answer using RISA (the first time I ever heard of the software). Of course, he was correct, it was his question.

I’ve been a bit bothered all these years, that I missed a question that was fairly easy to analyze but bothered also that the wrong answer seemed to prevail within the exam room (*). It certainly must have annoyed Dr. Kohutek.

In the PDF link, I present complete calculations:

Calculation of the horizontal reactions at the base of the columns
Calculation of the horizontal displacement at the beam level
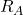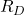First, I determine the base reactions $R_{A}$ and $R_{D}$ using the method of consistent deflections
Then I solve for $\Delta_{D}$ using the method of virtual work.
In this specific example:
The column length is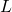 $L$ and the beam length is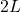 $2L$
All members are W8x24 steel beams
I place the 1 kip vertical load,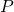 $P$ , at one-sixth of the beam length.
I also offer a graphical proof that the deflection is to the right.
See pages 17 through 20.
See the “Further Derivation” below for a closed form solution for 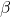$\beta$ such that $\Delta$ is maximum.
See the “General Solution” below for a closed form solution for 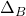$\Delta_{B}$ For any frame geometry.
As Vern Gosdin said, “That just about does it, don’t it”

(*) I guess we have all seen this happen in meetings.

Click for Asymmetric Frame Loading Calculations

Click for Influence Line

Of course, he was correct, it was his question.

Comparison of horizontal displacement results:

My hand calculation	Δ = 0.0384 inches
RISA-3D	Δ = 0.0387 inches
SAP2000	Δ = 0.0383 inches

Further Derivation

For the problem stated on Page 1 of the calculations, keeping $\beta$ as a variable,
I derived $\Delta_B$ in terms of $\beta$ :

$\boxed{\Delta_B=(1-2\beta)(1-\beta)\frac{\beta PL^3}{3EI}}$

Calculating $d\Delta_B}/{d\beta} = 0$ , and solving for $\beta_{m}$ where $\Delta_B$ is a maximum or minimum:

$\boxed{\beta_{m}=\frac{3\pm\sqrt{3}}{6}}$

$\beta_{m}=(0.21132, 0.78868)$

$\beta_{m}\cdot{24\text{'}}=(5.07\text{', }18.93\text{'})$

Using the $\beta_{m}$ value:

$\boxed{\Delta_B\text{ max}=(1-2\beta_{m})(1-\beta_{m})\frac{\beta_{m} PL^3}{3EI}}$

Remember, in our problem, $L$ is the height of the column, given in feet

$\Delta_B_{max}=0.032075\text{ }\frac{PL^3}{EI}\text{ feet}$

$\Delta_B_{max}=0.3849\text{ }\frac{PL^3}{EI}\text{ inches}$

Therefore, $\Delta_B_{max}=0.03994\text{ inches}}$ , which occurs when $P$ is located at $5.07\text{'}$ . These values are in agreement with the influence diagram determined using RISA-3D.

General Solution

Ultimately, I decided to develop a general solution. Below I present the general sketch, general parameters, and the general derivation. I also offer calculations for a specific example to allow comparison with commercial structural software.

In this general solution:

First, I use the method of consistent deflections to determine the base reactions 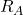$R_{A}$ and $R_{D}$
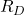
Then I use Castigliano’s 2nd Theorem, to solve for $\Delta_{D}$ .

The parameters are:

Parameter	Example Value
$L$ : length of the beam	24 feet
$\mu L$ : length of the two columns in the bent frame	varies
$A$ : distance from left support to point load	4 feet
$B$ : distance from right support to point load	20 feet
$\alpha$ : A/L	1/6
$\beta$ : B/L	5/6
$I$ : moment of inertia of beam	I=307 for W12x40
$\phi I$ : moment of inertia of columns	φ=1
$A$ : area of beam	A=11.7 for W12x40
$\theta A$ : area of columns	Θ=1

Click for General Formula calculations

Formula for deflection due to bending deformation in Cell 23

Formula for deflection due to axial deformation in Cell 30

When the $P$ load is centered (at $alpha = 1/2$ ), both formulas go to zero, as expected for a symmetric loading. What might not be expected, is that a horizontal displacement is generated by $P$ loadings at the column lines ( $\alpha = {0, 1}$ ). This horizontal displacement is solely the result of axial deformation in the columns.

Click for Tabular Results for the Example

For completeness

For completeness, here are three LIVE graphs:

Axial deflection along the beam

Bending deflection along the beam

Total deflection (axial + bending) along the beam

In the graphs, notice that there are 3 points specially marked along the beam; these represent the 3 alpha locations resulting in $\Delta_{D_{(axial + bending)}} = 0$ . Refer to the general formula calculations.

In this specific example:

$L = 12$ ‘

The column length is $L$ and the beam length is $2L$

Therefore, the column length is 12′ and the beam length is 24′

All members are W8x24 steel beams

Asymmetric Frame Loading Jul 2022

Leave a Reply Cancel reply

Recent Posts

Archives

QuickLinks