Homepage
>
Mathematics
>
Mental Math
>
On Average Jun 2022

On Average Jun 2022

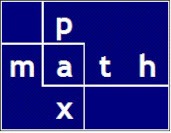
Here’s the whole story visually:

The rest is details.

Most everyone in math knows these tricks — here’s a summary of techniques used to make quick mental calculations of averages.

^† In the problems below, consider the residual,

R is defined as the remainder above or below the guessed average, aka, the residual.

RS is defined as the residual sum.

In school, I have 8 exam scores; what’s my average?
90
92
88
95
97
81
85
100
~~~
$\left. \begin{array}{ll} 90 \end{array} \right\}\text {say zero}$
$\left. \begin{array}{ll} 92\\ 88 \end{array} \right\}\text {say zero}$
$\left. \begin{array}{ll} 95\\ 97\\ 81 \end{array} \right\}\text {say 3}$
$\left. \begin{array}{ll} 85\\ 100 \end{array} \right\}\text {say 8}$

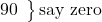
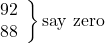
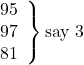
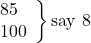
STEP by STEP (with explanation)
Guess maybe 90, then mentally calculate the running residual^† sum using two or three numbers at a time:

say zero (for 90: 90 is neither above or below the guessed average ∴R=0; ∴RS = 0),

say zero (for 92 and 88: the average of 92 and 88 is neither above or below the guessed average ∴R=0; ∴RS = 0),

say 3 (for 95, 97, and 81: ∴R = 5 + 7 – 9; ∴RS = 3),

say 8 (for 85 and 100: ∴R= -5 + 10 = 5; ∴RS = 8).

Answer: The average is 90 + 8/8 = 91.

Same problem — different guess. In school, I have 8 exam scores; what’s my average?

90
92
88
95
97
81
85
100
~~~
$\left. \begin{array}{ll} 90\\ 92\\ 88 \end{array} \right\}\text {say 15}$
$\left. \begin{array}{ll} 95\\ 97 \end{array} \right\}\text {say 37}$
$\left. \begin{array}{ll} 81\\ 85\\ 100 \end{array} \right\}\text {say 48}$

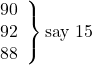
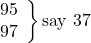
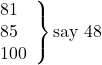
STEP by STEP (with explanation)
Guess maybe 85, then mentally calculate the running residual^† sum using two or three numbers at a time:

say 15 (for 90, 92, 88: ∴R = 5 + 7 + 3 = 15; ∴RS = 15),

say 37 (for 95 and 97: ∴R = 10 + 12 = 22; ∴RS = 37),

say 48 (for 81, 85, and 100: ∴R = -4 + 0 + 15 = 11; ∴RS = 48),

Answer: The average is 85 + 48/8 = 91.

Find average of 5 ‘hard numbers’ (with a lot of 9s, 8s, and 7s):

987
965
882
949
767
~~~
$\left. \begin{array}{ll} 987 \end{array} \right\}\text {say 13}$
$\left. \begin{array}{ll} 965 \end{array} \right\}\text {say 48}$
$\left. \begin{array}{ll} 949 \end{array} \right\}\text {say 99}$
$\left. \begin{array}{ll} 882 \end{array} \right\}\text {say 217}$
$\left. \begin{array}{ll} 767 \end{array} \right\}\text {say 450}$

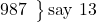
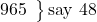
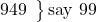
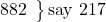
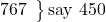
STEP by STEP (with explanation)
Assume a basis of 1000, mentally calculate the running residual^† sum:

say 13 (for 987: ∴R = -13; ∴RS = 13 down),

say 48 (for 965: ∴R = -35; ∴RS = 48 down),

say 99 (for 949: ∴R = -51; ∴RS = 99 down),

say 217 (for 882: ∴R = -118; ∴RS = 217 down),

say 450 (for 767: ∴R = -233; ∴RS = 450 down),

Answer: The average is 1000 – 450/5 = 910.

Incrementing an average, for example, I have 8 exam scores:

90
92
88
95
97
81
85
100

with an average of 91 (see Problem 1). Now I have a score of 78; what is my new average without re-summing?

Answer: It is simply 91 + (78 – 91)/9 = 91 – 13/9 = 89 5/9 = 89.55

Formula:

$prev\textunderscore n = 8$

$prev\textunderscore avg = 91$

$new\textunderscore n = 9$

$delta = new\textunderscore score - prev\textunderscore avg$

$delta = -13$

$\boxed{new\textunderscore avg = prev\textunderscore avg + \frac{delta}{new\textunderscore n}}$

[Powerful Formula] Incrementing an average, for example, I have 100 exam scores with an average of 87. Now I have a score of 100; what is my new average without re-summing?

Answer: It is simply 87 + (100 – 87)/101 = 87.1287

Incrementing an average, for example, I have 10,000 exam scores with an average of 87. Now I have a score of 100; what is my new average without re-summing?

Answer: It is simply 87 + (100 – 87)/10001 = 87.0013

[Very Powerful Formula] Incrementing an average, for example, I have 100 exam scores with an average of 87. Now I have 3 scores of {85, 80, 75}; what is my new average without re-summing?

87 – 85 = 2
87 – 80 = 7
87 – 75 = 12

Answer: It is simply 87 – (2 + 7 + 12)/103 = 86.7961

Determine the lowest allowable score to maintain a certain average. Say I have 8 scores with an average of 94. What is the least score on my 9th exam to maintain at least an average of 90?

Answer: It is 94 + (90 – 94) · 9 = 58.

Formula:

$prev\textunderscore n = 8$

$prev\textunderscore avg = 94$

$new\textunderscore n = 9$

$new\textunderscore avg = 90$

$delta = new\textunderscore avg-prev\textunderscore avg$

$delta = -4$

$\boxed{least\textunderscore score = prev\textunderscore avg + delta\cdot new\textunderscore n}$

[Very Very Powerful Formula] Determine the lowest allowable final exam score to maintain a certain average. Say I have 8 scores with an average of 94. What is the least score on my final exam to maintain at least a course grade of 90? Assume that the final exam is 40% of my course grade.

Answer: It is [90 – (94 x 0.6)]/0.4 = 84.

Formula:

$prev\textunderscore avg = 94$

$new\textunderscore avg = 90$

$final\textunderscore exam\textunderscore weight = 0.4$

$non\textunderscore final\textunderscore exam\textunderscore weight = 1-0.4$

$non\textunderscore final\textunderscore exam\textunderscore weight = 0.6$

$least\textunderscore score = \frac{new\textunderscore avg-(prev\textunderscore avg\cdot non\textunderscore final\textunderscore exam\textunderscore weight)}{final\textunderscore exam\textunderscore weight}$

[Wicked Powerful Formula] Alternative and easier formula:

$delta = new\textunderscore avg - prev\textunderscore avg$

$\boxed{least\textunderscore score = prev\textunderscore avg+\frac{delta}{final\textunderscore exam\textunderscore weight}}$

So, how much does a 100 raise your average?

Formula:

$variance = 100 - prev\textunderscore avg$

$\boxed{change\textunderscore avg = \frac{variance}{new\textunderscore n}}$

Enjoy!

Leave a Reply Cancel reply