Transform Axes Jun 2021

Here is yet another presentation about a VBA function that was recoded in Python.

In structural engineering, we must constantly deal with axes transformations.  Mostly we have right handed coordinates (RHC), but sometimes left handed coordinates (LHC). For example, LHCs might occur when South or East map coordinates are used. Certain engineering software packages use LHC.

A few quick questions:

• How many XYZ orientations are there?
  (48)
• How many RHC XYZ orientations are there?
  (24)
• How many LHC XYZ orientations are there?
  (24)

Conceptual proof:

• Imagine the XYZ system in your head
• Label the directions 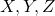as 1, 2, 3
• Label the directions 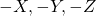as 4, 5, 6
  
• Now imagine transforming 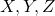to .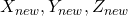
• Let’s say 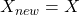(∴ 1) and 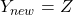(∴ 3)
• We could use the two digit notation [13] for the new system orientation
• There are 4 orientations starting with 1:
  • [12]:
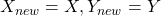
  • [13]:
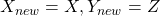
  • [15]:
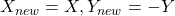
  • [16]:
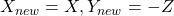
  • [11]: isn’t legal. 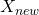and 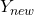must have different directions
  • [14]: isn’t legal. 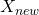and 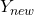cannot be in opposite directions
• Consider then two digit orientations 2_, 3_, 4_, 5_, 6_
• For each of these we can have four orientations
• Therefore, there are 24 RHC orientations; 6 choices for 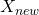times 4 choices for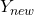
• Therefore, there are 24 RHC orientations
• Then allow RHC or LHC orientations
• Therefore, there are 24 LHC orientations
• Therefore, there are 48 total orientations

This makes it almost trivial to think through the transformation desired.

Given a point , to make the RHC transformation we simply execute a single rotation about a single vector:

• to produce [12]: rotate 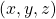zero degrees about vector 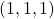## no change
• to produce [15]: rotate 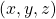180 degrees about vector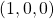
• to produce [13]: rotate 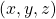90 degrees about vector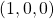
• to produce [16]: rotate 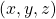270 degrees about vector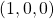

• to produce [43]: rotate 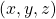180 degrees about vector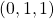
• to produce [46]: rotate 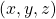180 degrees about vector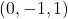

Click here to link http://motion.cs.illinois.edu/RoboticSystems/3DRotations.html (see Item 5)

To make the LHC transformation we negate the Z-axis coordinate of the output point after rotating the point about the vector.

For my transformation function, I predetermined the vectors and rotations for the 24 RHC orientations.

Using PyXLL, the function is callable from Excel.

Another example

Rotation matrix and rotation equation for [23]: (∴ 2) and (∴ 3)

Excel spreadsheet PDF

In row 19, notice that a single PyXLL function call takes a single orientation input [23], calculates the rotation matrix once, and performs a block of point transformations in a single matrix equation. Yep, that’s a screenshot from an iPhone.
Click here to see full PDF

https://sites.google.com/site/glennmurray/glenn-murray-ph-d/rotation-matrices-and-formulas
https://en.wikipedia.org/wiki/Rotation_matrix#Rotation_matrix_from_axis_and_angle
https://en.wikipedia.org/wiki/Levi-Civita_symbol

Rotation matrix from axis and angle

The matrix of a proper rotation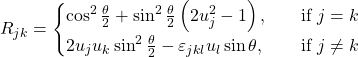 by angle around the axis , a unit vector with , is given by:

where is the Levi-Civita symbol with