Often while working, an arithmetical answer is needed — exact is sometimes required, approximate is often acceptable — maybe the basis of a decision or a path forward is based on a few quick calculations, with more rigorous calculations to follow
Let’s illustrate with examples from two groups
First, we’ll learn to multiply by 11 by just writing down the answer
Question: What is 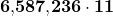 ?
?
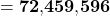
Try it by yourself this time
Solution:
Try it by yourself this time
Remember the binomial theorem or Pascal’s Triangle. Let’s go back a few years and refresh.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Second, we’ll try a few exponent calculations
Question: What is 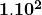 ?
?
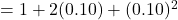
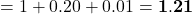
Solution:
And 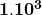 ?
?
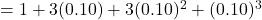
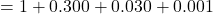
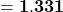
Solution:
Question: What is 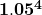 ?
?
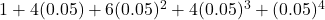
Now dropping the last two terms, we have
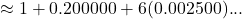
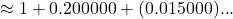
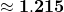
Solution:
Now dropping the last two terms, we have
The exact answer is 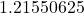
Therefore, by using only three terms we have an error of less than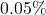
Therefore, by using only three terms we have an error of less than
Now let’s consider a few squares.
Question: What is 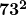 ?
?
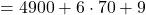
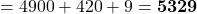
Recall that ![]()
Solution: ![]()
Question: What is 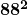 ?
?
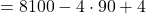

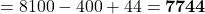
Recall that ![]()
Solution: ![]()
Question: What is 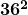 ?
?
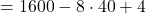
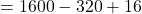
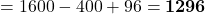
Again ![]()
Solution: ![]()
Now let’s consider common temperature conversions.
Start with determining the Fahrenheit equivalent of a Centigrade temperature ?
Recall 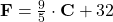
Or![Rendered by QuickLaTeX.com \bold{F} = [1.80] \cdot \bold{C}+32](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-a2717a95414a33c56933d4e8794042f2_l3.png)
Easier if approached using![Rendered by QuickLaTeX.com \bold{F} = [0.90 \cdot 2] \cdot \bold{C}+32](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-e674b40c13e38f9f25cd086e06f19427_l3.png)
Which is simply![Rendered by QuickLaTeX.com [2 \cdot \bold{C}]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-e3cd1619c8a979524a3b349a171cd437_l3.png) less
less 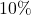 plus
plus 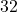
Or
Easier if approached using
Which is simply
Question: What is the Fahrenheit equivalent of 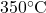 ?
?
Say ![Rendered by QuickLaTeX.com [2 \cdot \bold{350}]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-f1750b2b91d58de46b973f1c5abffa91_l3.png) less
less 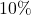 plus
plus 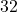
Say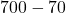 plus
plus 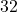
Say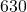 plus
plus 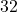
Therefore,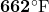
Say
Say
Therefore,
Recall 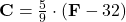
Or![Rendered by QuickLaTeX.com \bold{C} = [0.55\bar5] \cdot [\bold{F}-32]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-d3b20eed2c1a2823cf1b52cfade697e2_l3.png)
Easier if approached using![Rendered by QuickLaTeX.com \bold{C} = [0.50+(0.1) \cdot 0.50+(0.01) \cdot 0.50] \cdot [\bold{F}-32]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-e212b036b9f0ba94a1a719cde98801e9_l3.png)
So say![Rendered by QuickLaTeX.com [\bold{F}-32]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-f4a10f752e41a820279ad2ea606cec7c_l3.png) times half plus
times half plus ![Rendered by QuickLaTeX.com [\bold{F}-32]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-f4a10f752e41a820279ad2ea606cec7c_l3.png) times a tenth of a half and so forth
times a tenth of a half and so forth
Or
Easier if approached using
So say
Question: What is the Centigrade equivalent of 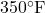 ?
?
Say ![Rendered by QuickLaTeX.com [350-32] = 318](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-6f5477cf07d99ad8bd391ede7458ac7a_l3.png)
Say half of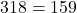
Say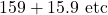
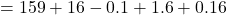
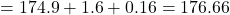
Therefore,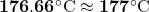 .
.
Say half of
Say
Therefore,
Question: What is the Centigrade equivalent of 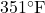 ?
?
Say ![Rendered by QuickLaTeX.com [351-32] = 319 \text{ (odd number)}](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-85a03be8635429bb8a4cc592db45cc7c_l3.png)
Say half of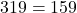 with a remainder of
with a remainder of 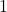
Say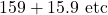
![Rendered by QuickLaTeX.com = 159+16-0.1+1.6+0.16+[0.6]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-008d62a298547df5febdb5e699c4234a_l3.png)
![Rendered by QuickLaTeX.com = 176.66+[0.6]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-1513b860cf525e04b46bd6820d82c529_l3.png)
Say half of
Say
The extra 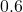 is to account for the remainder of 1
is to account for the remainder of 1
Therefore, 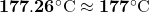 .
.
Question: What is the Centigrade equivalent of 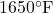 ?
?
Say ![Rendered by QuickLaTeX.com [1650-32] = 1618}](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-c87c91ff219daed450c8ae8f088a57c3_l3.png)
Say half of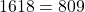
Say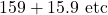
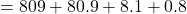
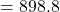
Therefore,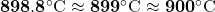 .
.
Say half of
Say
Therefore,
And last, Aliquot Parts
2, 5
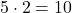
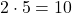 To multiply by 2, we can divide by 5 if it’s easier that way
To multiply by 2, we can divide by 5 if it’s easier that way
2, 50
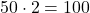
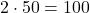
4
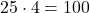
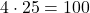
To multiply by 25, we can divide by 4 if it’s easier that way
To divide by 25, we can multiply by 4 if it’s easier that way
8
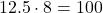
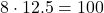
3
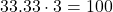
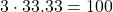
6
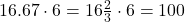
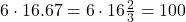
7
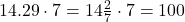
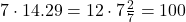
9
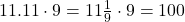
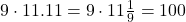
12
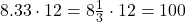
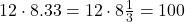
15
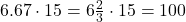
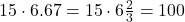
Click for a couple three quick examples using aliquot parts
How to use the divisors of 1, of 10, and of 100
2, 5
To multiply by 5, we can divide by 2 and vice versa, whichever is easier!
What is 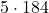 ?
?
Just say 184 over 2 times 10; therefore, 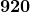 .
.
What is 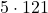 ?
?
Just say 121 times 5; therefore, 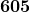 .
.
What is 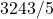 ?
?
Just say 3243 times 2 over 10; therefore, 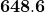 .
.
What is 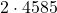 ?
?
Just say 4585 over 5 times 10; therefore, 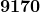 .
.
What is 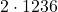 ?
?
Just say 1236 times 2; therefore, 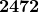 .
.
2, 50
5, 20
![]()
![]()
4
To multiply by 25, we can divide by 4 if it’s easier that way
What is 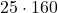 ?
?
Just say 160 over 4 times 100;
therefore,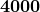 .
.
therefore,
What is 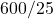 ?
?
Just say 6 times 4;
therefore,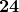 .
.
therefore,
8
3
6
7
9
12
What is 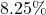 tax on
tax on 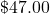 ?
?
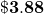
Just say 47 over 12; therefore, ~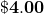
Could say 47 over 12 less say ~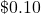 ;
;
therefore, ~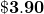 .
.
The exact value is Could say 47 over 12 less say ~
therefore, ~
15
![]()
![]()
What is 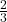 of
of 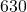 ?
?
Just say 630 over 15 times 10; therefore, 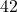 times
times 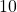 ; therefore,
; therefore, 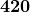 .
.
Click for a couple three quick examples using aliquot parts