Uncertainty Analysis
To illustrate a simple but often ignored concept – what is the estimated total cost of the following?
| Item | Cost | |
|---|---|---|
| alpha | 100,000 | 5,000 |
| beta | 75,000 | 7,500 |
| gamma | 50,000 | 6,000 |
| .. | .. | .. |
| total | 225,000 | what is the total plus-minus range? |
I say the answer is:
| Item | Cost | |
|---|---|---|
| .. | .. | .. |
| total cost | 225,000 | 11,000 (10,828) |
Notice that the plus-minus range for the total cost is less than the sum of the plus-minus ranges. This will always be true when adding in quadrature.
![]()
Uncertainty Analysis Reference — Summary of Error Propagation [Harvard]
I first read about this approach in Excel Best Practices for Business by Loren Abdulezer.
Abdulezer, Loren. ”Chapter 8 — Analyzing Data.” Excel Best Practices for Business, edited by Susan Christopherson, Wiley Publishing Inc, 2004, pp. 220–229.
In accordance with the rules of quadrature, our uncertainty is:
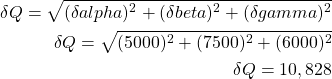
The quantities alpha, beta, and gamma must have uncertainties which are uncorrelated and random.
Example Calculation
If say ![]() same-cost items were considered, with a constant
same-cost items were considered, with a constant ![]() percent plus-minus cost:
percent plus-minus cost:
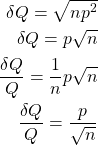
![]()
If ![]() items of a uniform random cost (and still independent variables) were considered, with a constant
items of a uniform random cost (and still independent variables) were considered, with a constant ![]() percent (
percent (![]() ) plus-minus cost, we might calculate
) plus-minus cost, we might calculate ![]() percent instead of
percent instead of ![]() percent.
percent.
I did compress the WAV file — from 56 MB to 19 MB. I’ve noticed very slight glitches in the compressed version.
Adding in quadrature is a method used to calculate the total uncertainty of a sum when the individual uncertainties are uncorrelated. It involves taking the square root of the sum of the squares of the individual uncertainties. This method is used in engineering cost estimation.
Here’s a breakdown of key concepts related to adding in quadrature:
- Core Principle: Adding in quadrature recognizes that individual uncertainties may offset each other rather than simply accumulating arithmetically.
- Uncorrelated Uncertainties: A critical condition for using adding in quadrature is that the uncertainties of the individual items must be uncorrelated and random. Uncorrelated means that the errors or variations of one item do not depend on the errors or variations of another.
- Why not simple addition: The total cost uncertainty calculated using adding in quadrature is less than the simple sum of individual cost uncertainties. This is because individual uncertainties are likely to partially cancel each other out.
- Impact on Percentage Uncertainty: When many items of the same cost are considered, the percentage uncertainty in the total cost is reduced. Similarly, when items have a uniform random cost, the percentage uncertainty in the total cost might be lower compared to the percentage uncertainty of each item.
In summary, adding in quadrature is a valuable tool for estimating total cost uncertainty, especially when dealing with uncorrelated individual uncertainties. It provides a more realistic estimate than simply adding up the uncertainties.
Key Terms
Uncorrelated: In the context of uncertainties, uncorrelated means that the individual errors or variations do not have a relationship where the fluctuation of one depends on the fluctuation of another.
Uncertainty Analysis: The process of evaluating and quantifying the possible range of error in a measurement or estimate.
Significant Digits: The digits in a number that carry meaning contributing to its precision.
Random Uncertainty: Errors or variations that occur unpredictably in any direction.
Percentage Uncertainty: The uncertainty of a measurement or estimate expressed as a percentage of the value.
Propagation of Uncertainty: The process of determining how uncertainty in one or more variables affects the uncertainty of a dependent variable.
Uniform Random Cost: A type of variable where every value within a specified range is equally likely to occur.
NotebookLM can be inaccurate, please double check its responses.