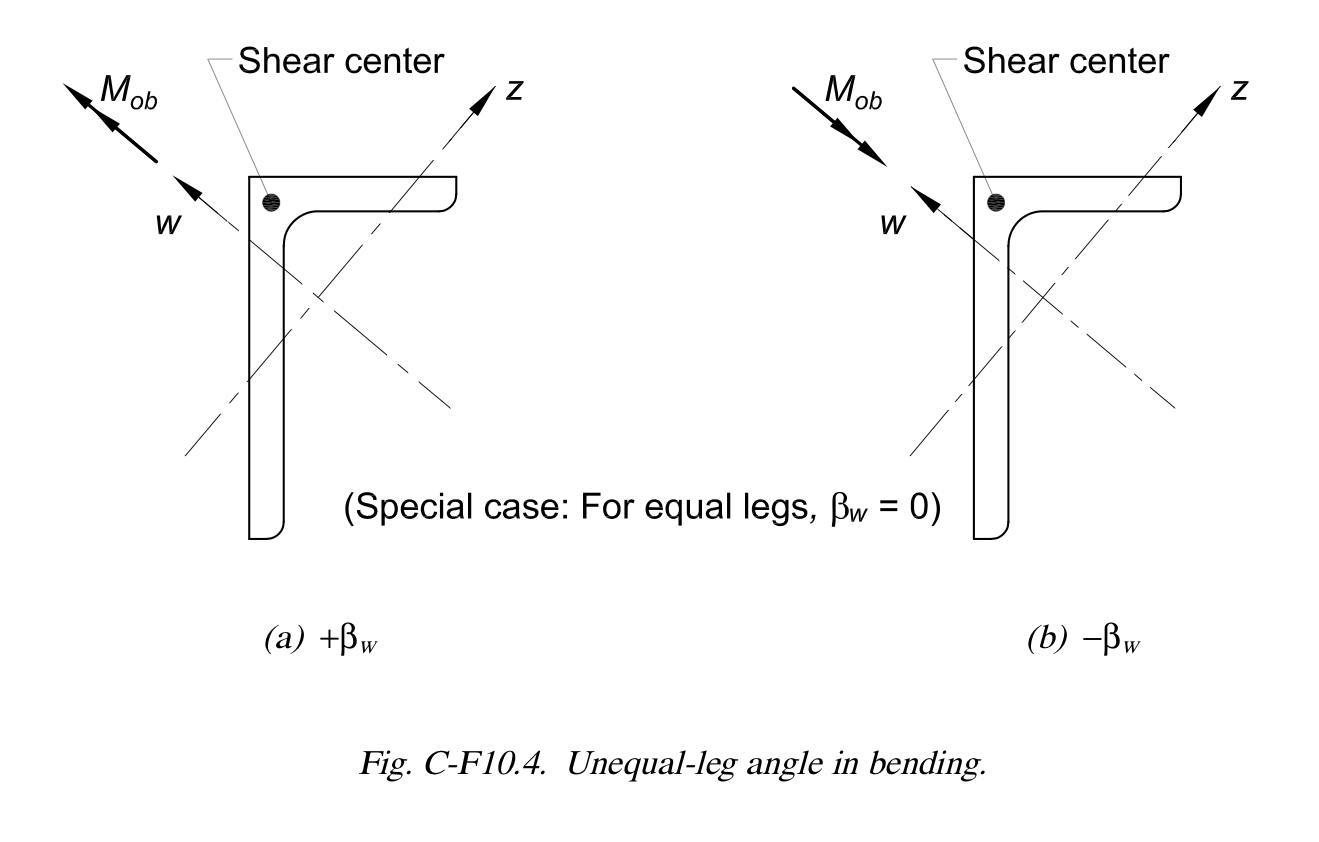
Algebraic formula for AISC property, Beta w
I used the Python package sympy
to develop a closed form solution
for beta w.
Thank you to AISC.
Thank you to https://fr.maplesoft.com/index.aspx
Thank you to slideshare presentation.
to develop a closed form solution
for beta w.
Thank you to AISC.
Thank you to https://fr.maplesoft.com/index.aspx
Thank you to slideshare presentation.

'''
NOTE
For enhanced readability and easier translation to other software,
exponents are indicated with the (mathematically) traditional caret symbol.
In Python, replace all carets with a double asterisk.
In Excel, replace all references to 'c' with 'c_'.
Refer to https://www.excelforum.com/excel-general/1205767-cannot-name-a-cell-as-c.html
You cannot use R, C, r, or c as range names as they conflict with the RC addressing style.
The workaround is not to use just R or C — perhaps R_ or C_.
The workaround is not to use just r or c — perhaps r_ or c_.
Get single angle properties
a = np.arctan(my_angle.TANA)
c = np.cos(a)
s = np.sin(a)
b = my_angle.B_LOWERCASE
d = my_angle.D
g = my_angle.X
h = my_angle.Y
t = my_angle.T
'''
z0 = -s*(t/2 - g) + c*(t/2 - h)
Iw = my_angle.IW
# B is the integral term shown above
# Then set
# B12 = 12 * B
# To avoid fractional coefficients from the expansion of B
# Now calculate B12, a lengthy expression
# Obviously, many of the terms may be grouped further
# Dec 2019: Such grouping is not a priority for me
# Jul 2021: Using Maplesoft Maple 2021, I obtained a couple equivalent
# but more succinct expressions for B12.
##########
# Jul 2021 Version A
# Polynomial terms are collected in powers of t
B12 = (-5*c + 5*s)*t^5 + (-3*b*s + 3*c*d + 6*c*g + 16*c*h - 16*g*s - 6*h*s)*t^4
+ (2*b^2*c - 4*b*c*h + 12*b*g*s - 12*c*d*h - 6*c*g^2 - 12*c*g*h
- 18*c*h^2 - 2*d^2*s + 4*d*g*s + 18*g^2*s + 12*g*h*s + 6*h^2*s)*t^3
+ (-2*b^3*s - 6*b^2*c*g + 6*b^2*h*s + 12*b*c*g*h - 18*b*g^2*s
- 6*b*h^2*s + 2*c*d^3 - 6*c*d^2*g + 6*c*d*g^2 + 18*c*d*h^2
+ 12*c*g^2*h + 12*c*h^3 + 6*d^2*h*s - 12*d*g*h*s - 12*g^3*s
- 12*g*h^2*s)*t^2
+ (3*b^4*c - 12*b^3*c*h + 4*b^3*g*s + 6*b^2*c*g^2 + 18*b^2*c*h^2
- 12*b^2*g*h*s - 12*b*c*g^2*h - 12*b*c*h^3 + 12*b*g^3*s + 12*b*g*h^2*s
- 4*c*d^3*h + 12*c*d^2*g*h - 12*c*d*g^2*h - 12*c*d*h^3 - 3*d^4*s
+ 12*d^3*g*s - 18*d^2*g^2*s - 6*d^2*h^2*s + 12*d*g^3*s + 12*d*g*h^2*s)*t
##########
# Jul 2021 Version B
# Powers of t are not collected; minimal references to c and s
# I added an extra plus sign to visually separate the two terms.
B12 = 3*t*((-(5*t^4)/3 + (2*g + (16*h)/3 + d)*t^3
+ (-2*g^2 - 4*g*h - 6*h^2 + (-(4*b)/3 - 4*d)*h + (2*b^2)/3)*t^2
+ ((2*d + 4*h)*g^2 + (-2*b^2 + 4*b*h - 2*d^2)*g + 6*d*h^2
+ (2*d^3)/3 + 4*h^3)*t + ((-4*b - 4*d)*h + 2*b^2)*g^2
+ 4*d^2*g*h + (-4*b - 4*d)*h^3 + 6*b^2*h^2 + (-4*b^3 - (4*d^3)/3)*h + b^4)*c
+
+ (4*s*((5*t^4)/4 + (-(3*b)/4 - 4*g - (3*h)/2)*t^3
+ ((9*g^2)/2 + (3*b + d + 3*h)*g - d^2/2 + (3*h^2)/2)*t^2
+ (-3*g^3 - (9*b*g^2)/2 - 3*h*(d + h)*g - (3*b*h^2)/2
+ ((3*b^2)/2 + (3*d^2)/2)*h - b^3/2)*t + (3*b + 3*d)*g^3
- (9*d^2*g^2)/2 + ((3*b + 3*d)*h^2 - 3*b^2*h + b^3
+ 3*d^3)*g - (3*d^4)/4 - (3*d^2*h^2)/2))/3)
##########
# Dec 2019
# As published in my original post.
B12 = t^5*(5*s^3 -5*s^2*c +5*s*c^2 -5*c^3) +
t^4*(-6*s^3*h -16*s^3*g -3*s^3*b -6*s*c^2*h -16*s*c^2*g
-3*s*c^2*b +16*s^2*c*h +6*s^2*c*g +3*s^2*c*d +16*c^3*h
+6*c^3*g +3*c^3*d) +
t^3*(6*s^3*h^2 +12*s^3*h*g +18*s^3*g^2 +12*s^3*g*b +4*s^3*g*d -2*s^3*d^2
-18*s^2*c*h^2 -12*s^2*c*h*g -4*s^2*c*h*b -12*s^2*c*h*d -6*s^2*c*g^2
+2*s^2*c*b^2 +6*s*c^2*h^2 +12*s*c^2*h*g +18*s*c^2*g^2 +12*s*c^2*g*b
+4*s*c^2*g*d -2*s*c^2*d^2 -18*c^3*h^2 -12*c^3*h*g -4*c^3*h*b
-12*c^3*h*d -6*c^3*g^2 +2*c^3*b^2) +
t^2*(-12*s^3*h^2*g -6*s^3*h^2*b -12*s^3*h*g*d +6*s^3*h*b^2 +6*s^3*h*d^2
-12*s^3*g^3 -18*s^3*g^2*b -2*s^3*b^3 -12*s*c^2*h^2*g -6*s*c^2*h^2*b
-12*s*c^2*h*g*d +6*s*c^2*h*b^2 +6*s*c^2*h*d^2 -12*s*c^2*g^3
-18*s*c^2*g^2*b -2*s*c^2*b^3 +12*s^2*c*h^3 +12*s^2*c*h*g^2
+12*s^2*c*h*g*b +18*s^2*c*h^2*d -6*s^2*c*g*b^2
-6*s^2*c*g*d^2 + 6*s^2*c*g^2*d +2*s^2*c*d^3 +12*c^3*h^3
+12*c^3*h*g^2 +12*c^3*h*g*b + 18*c^3*h^2*d -6*c^3*g*b^2
-6*c^3*g*d^2 +6*c^3*g^2*d +2*c^3*d^3) +
t*(12*s^3*h^2*g*b +12*s^3*h^2*g*d -6*s^3*h^2*d^2 -12*s^3*h*g*b^2
-18*s^3*g^2*d^2 +4*s^3*g*b^3 +12*s^3*g*d^3 +12*s^3*g^3*b +12*s^3*g^3*d
-3*s^3*d^4 +12*s*c^2*h^2*g*b +12*s*c^2*h^2*g*d -6*s*c^2*h^2*d^2
-12*s*c^2*h*g*b^2 -18*s*c^2*g^2*d^2 +4*s*c^2*g*b^3 +12*s*c^2*g*d^3
+12*s*c^2*g^3*b +12*s*c^2*g^3*d -3*s*c^2*d^4 -12*s^2*c*h^3*b
-12*s^2*c*h^3*d -12*s^2*c*h*g^2*b -12*s^2*c*h*g^2*d +12*s^2*c*h*g*d^2
-12*s^2*c*h*b^3 -4*s^2*c*h*d^3 +18*s^2*c*h^2*b^2 +6*s^2*c*g^2*b^2
+3*s^2*c*b^4 -12*c^3*h^3*b -12*c^3*h^3*d -12*c^3*h*g^2*b -12*c^3*h*g^2*d
+12*c^3*h*g*d^2 -12*c^3*h*b^3 -4*c^3*h*d^3 +18*c^3*h^2*b^2
+6*c^3*g^2*b^2 +3*c^3*b^4)
# From definition
B = B12 / 12.0
# Therefore
Beta_w = B / Iw - 2*z0
# Using a few example shapes with corresponding data from the
# AISC v15.0 Shapes database
Beta_w = 3.2879 for L8x6x1
Beta_w = 3.3139 for L8x6x1/2
Beta_w = 3.3246 for L8x6x7/16
Beta_w = 1.5653 for L3x2x5/16

THIS IS FABULOUS, THANK YOU FOR THIS WORK!
Thanks, Shawn — I appreciate the feedback.