I present a few problems
- Given a cantilever subject to three separate loadings:
(a) a concentrated load P at the free end,
(b) a moment M at the free end, and
(c) a uniform load w over the entire beam.
The span is L.
For each loading, determine the beam deflection at the free end of the span.
Answer: (a)![Rendered by QuickLaTeX.com \[\delta = \frac{PL^3}{3EI}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-dbcfa1b8b55b9ca4acf4b52f1360ee36_l3.png)
Answer: (b)
![Rendered by QuickLaTeX.com \[\delta = \frac{ML^2}{2EI}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-1984f17a0f4e0ac8e8bc46d0de81c63f_l3.png)
Answer: (c)
See calculation of cantilever deflections![Rendered by QuickLaTeX.com \[\delta = \frac{wL^4}{8EI}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-cb304ff8925e7d16aa96ec2a0181cc09_l3.png)
- Given a simple beam with a P load at midspan.
The span is L.
Determine the beam rotation at the right end of the span.
Answer:![Rendered by QuickLaTeX.com \[\theta_{B} = \frac{PL^2}{16EI}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-5d21ff3b3d2e40dbcdb33d5623dee52b_l3.png)
See calculation of symmetric rotation
I solved this problem using the virtual work method.

- Given a simple beam with a P load at at a distance a from the left support.
The span is L; therefore,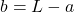 .
.
Determine the beam rotation at the right end of the span.
Determine also the deflection for all points x located left of the P loading.
Answer:![Rendered by QuickLaTeX.com \[\theta_{B} = \frac{Pab(L+a)}{6EIL}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-a0bf352cbe58b8b3bbf7ab973a0ca659_l3.png)
See calculation of asymmetric rotation
I solved this problem using the conjugate beam method (*).

Note that if![Rendered by QuickLaTeX.com \[a = \frac{L}{2}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-1fcdcd7bd0a747d01bf47127e0d8ba39_l3.png)
![Rendered by QuickLaTeX.com \[\text{and therefore}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-e203f4812cfbaebdc411b7fb4638a5da_l3.png)
![Rendered by QuickLaTeX.com \[b = \frac{L}{2}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-b7333ed8eadaac55bc27b6126a33197c_l3.png)
then the third equation is equal to the second equation.
- Given a beam (or plate) with uniform load, w, subjected to a 2 point symmetric lift
The center span, L, is to be determined
The value, a, is a ratio to be determined
The left overhang = the right overhang =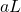

Determine the span and the overhang that minimizes the absolute value of the moment along the span
Answer: see calculation of lift load points
Determine the resulting deflection at the right end of the beam, at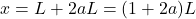
Answer: see hand calculation of deflection given minimized moment
Answer: see calculation of deflection given minimized moment using sympy.physics.continuum_mechanics.beam.Beam (**)
Note that my calculation of a agrees with the well-known value of a.![Rendered by QuickLaTeX.com \[a=0.3536\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-e6ea8eae2f178524250805e2af994f12_l3.png)
I derived two deflection equations:![Rendered by QuickLaTeX.com \[\frac{aL}{L+2aL} = \frac{a}{1+2a} = \frac{\sqrt{2}-1}{2} \approx 0.2071 \approx 0.21\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-9ee8a10b229c690e672369511addc0b4_l3.png)
![Rendered by QuickLaTeX.com \[\Delta_{cantilever}=\frac{a(1-6{a}^2-3{a}^3)}{24}\frac{{w}{L}^4}{{E}{I}}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-4ae3fffd655d5b18bf63db6704edc872_l3.png)
![Rendered by QuickLaTeX.com \[\Delta_{centerspan}=\frac{(6{a}^2-1)}{48}\frac{{w}{L}^4}{{E}{I}}\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-35b0f5f2145a248ffc16c5ca229a1fdb_l3.png)
See calculation of centerspan deflection.
I determined a few interesting values of a and charted the resulting deflections.
See calculation of cantilever deflection.
- Given a pin-supported bent with uniform EI:
The beam span is L.
The column length is μL.
Determine the horizontal deflection of the frame at point B.
Answer:
See calculation of frame deflection![Rendered by QuickLaTeX.com \[\Delta_{B} = \Big( \frac{\mu^2L^3(1+2\mu)}{12EI}\Big) H\]](https://www.mathpax.com/wp-content/ql-cache/quicklatex.com-53d1cc274bf0278790bf4ecf7292530c_l3.png)
Bonus Material
For the first 2 problems, I checked some algebra using Jupyter, Plotly, Python, and Sympy.
http://khoitsmahq.firstcloudit.com/images%2Fbeam_hand_calc_check.html
Additional Bonus Material
Quite a surprise — I discovered a Sympy package named sympy.physics.continuum_mechanics.beam.Beam (**) and checked some of my results using that package too. Note Sympy’s use of singularity functions in cells 4 and 5. I use singularity functions in cells 6 through 10.
http://khoitsmahq.firstcloudit.com/images%2Fshear_and_moment.html
def f_rotation(x, E, I):
sf = SingularityFunction
return (-10*sf(x, 0, 2)/3 +
5*sf(x, 48, 2) -
5*sf(x, 144, 2)/3 +
12800)/(E*I)
def f_deflection(x, E, I):
sf = SingularityFunction
return (12800*x -
10*sf(x, 0, 3)/9 +
5*sf(x, 48, 3)/3 -
5*sf(x, 144, 3)/9)/(E*I)
References
(*) Conjugate Beam Method — Wiki
(**) https://docs.sympy.org/… continuum_mechanics/beam.html
(***) A bonus from Dr. Myosotis