Major League Baseball Batting Champions
In 1945 in the American League, George “Snuffy” Stirnweiss (NYY) edged out Tony Cuccinello (CHW) for the league batting championship.
I wondered how close two batting averages could be.
I built an exhaustive search(*) Python program, and I found:
Analysis of the Gap Distribution
Stirnweiss had 195 hits in 632 at-bats for a 0.3085443 average.
Cuccinello had 124 hits in 402 at-bats for a 0.3084577 average.
The difference was 0.0000866 (about 90 millionths) !
I found that interesting as a baseball fact, and as a mathematical occurrence: that two 3-digit rational fractions are that close together.Cuccinello had 124 hits in 402 at-bats for a 0.3084577 average.
The difference was 0.0000866 (about 90 millionths) !
I wondered how close two batting averages could be.
I built an exhaustive search(*) Python program, and I found:
The minimum difference in adjacent averages, for averages less than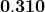 
with 
, we ha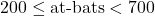ve
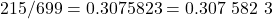
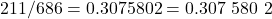
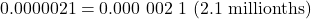
with , we haveand
for a difference of
and
The minimum difference in adjacent averages, for averages less than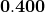 
with , we have
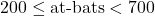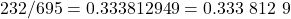
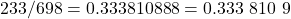
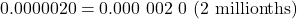
with , we haveand
for a difference of
Analysis of the Gap Distribution
Here is a quick summary of the gaps between adjacent batting averages less than with .
| Gap | Frequency of Gap Occurrence |
|---|---|
| 0 to 2 millionths | 0.0% |
| 2 to 4 millionths | 14.5% |
| 4 to 8 millionths | 23.2% |
| 8 to 16 millionths | 35.6% |
| 16 to 32 millionths | 18.7% |
| 32 to 64 millionths | 5.5% |
| 64 to 128 millionths | 1.9% |
| 128 to 256 millionths | 0.4% |
| 256 to 512 millionths | 0.2% |
Bonus Feature
Link to alternate live Plotly chart (bins are all of equal size, 2 millionths) (a bit slow loading)
and
The maximum difference in adjacent averages, for averages less than 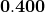with , we have
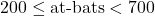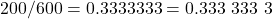
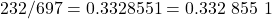
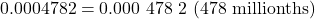
with , we haveand
for a difference of
~~~
Year by Year Leaders for Batting Average
The Way the Game Is Supposed to Be Played: George Kell, Ted Williams, and the battle for the 1949 batting title (a good story)
The Way the Game Is Supposed to Be Played: George Kell, Ted Williams, and the battle for the 1949 batting title (a good story)
(*) The exhaustive search was as follows: generate all possible batting averages over the specified range, sort, filter out all duplicate averages (for example 200/600, 201/603), determine gaps between adjacent averages.
